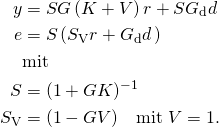Vorwort
Dies ist der zweite Teil zu der „Stationären Vorsteuerung“. Teil 1 führt die Idee ein und zeigt, dass immer Überschwingen resultiert:
Hier, im zweiten Teil, schauen wir auf „Performance“. Die ist natürlich erstmal schlecht, weil ja immer Überschwingen entsteht. Nichtsdestotrotz könnte irgendein Performancegewinn entstehen, Überschwingen hin oder her. Das ist die Frage, die wir jetzt stellen.
Ein Kommentar: ,,Performance“ ist die übliche Wortwahl in der Industrie für „Regelfolgeverhalten“. So verstehen wir das hier auch.
Zusammenfassung
Dieser Blog-Artikel geht mathematisch ein bissl ins Eingemachte — das heißt er ist für Experten gedacht. Für die Leser, die sich die Mathematik unten sparen wollen, folgende Zusammenfassung:
Die Stationäre Vorsteuerung hilft nur bei passiven (SPR) Strecken und selbst dort nur homöopathisch. In allen anderen Fällen hilft sie nicht, sondern schadet immens. Finger weg, davon!
Untersuchte Regelkreisstruktur
Unser Ziel: Verstehen, wie sich die Stationäre Vorsteuerung auf den Regelfehler auswirkt und das möglichst allgemein bewerten.
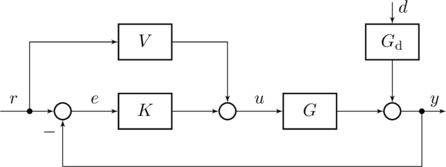
Abbildung 1: Standardregler mit Stationärer Vorsteuerung.
Aus Abbildung 1 ergeben sich folgende Zusammenhänge:
(1)
![]() in den Gleichungen zeigt, wo die Vorsteuerung wirkt. Wichtig für die folgenden Überlegungen ist, dass der Regelfehler durch die Stationäre Vorsteuerung mit
in den Gleichungen zeigt, wo die Vorsteuerung wirkt. Wichtig für die folgenden Überlegungen ist, dass der Regelfehler durch die Stationäre Vorsteuerung mit ![]() verändert wird.
verändert wird.
Wir erinnern uns (aus dem Teil 1), dass wir einen allgemeinen, vereinfachten Fall annehmen dürfen:
Ohne Beschränkung der Allgemeinheit wird im Folgenden angenommen, dass die stationäre Verstärkung der Strecke eins ist (
). Daraus folgt, dass die stationäre Vorsteuerung (in diesem Fall) ebenso eins ist (
).
Wirkung auf die Performance
Wir stellen folgende Frage:
Gegeben ist (irgend-)ein Standardregler
. Verbessert die stationäre Vorsteuerung die Performance?
Es gilt: je ,,kleiner“ der Regelfeher ![]() , desto besser. Wir betrachten die Wirkung des Sollwertes
, desto besser. Wir betrachten die Wirkung des Sollwertes ![]() auf den Regelfehler
auf den Regelfehler ![]() . Wir schlagen uns auf die Seite der Stationären Vorsteuerung, indem wir fragen: Wann hilft sie?
. Wir schlagen uns auf die Seite der Stationären Vorsteuerung, indem wir fragen: Wann hilft sie?
Zur Erinnerung (mit ![]() ):
):
![]()
Der Effekt der Stationären Vorsteuerung geht also über ![]() in den Regelfehler ein.
in den Regelfehler ein.
Variante 1: Regelfehler ,,klein“ bei jeder Frequenz
Möchte man kleine Regelfehler, so muss der Ausdruck ![]() kleiner 1 sein. Selbst wenn beim Zuschalten der stationären Vorsteuerung über alle Frequenzen der Regelfehler kleiner wird, so kann die Sprungantwort dennoch überschwingen. Es besteht also kein Widerspruch zu dem immer gegebenen Überschwingen.
kleiner 1 sein. Selbst wenn beim Zuschalten der stationären Vorsteuerung über alle Frequenzen der Regelfehler kleiner wird, so kann die Sprungantwort dennoch überschwingen. Es besteht also kein Widerspruch zu dem immer gegebenen Überschwingen.
Für eine Regelstrecke ohne Pole auf der imaginären Achse muss gelten
(2)
damit die stationäre Vorsteuerung einen positiven Effekt hat für Sollwerte der Frequenz
.
Falls der Ausdruck aber größer eins ist, so ist die stationäre Vorsteuerung destruktiv.
Ungleichung (2) hilft scheinbar nicht viel. Die Erkenntnis ist jedoch, dass die Wirkung der stationären Vorsteuerung abhängig von der Regelstrecke ist!
Jetzt können wir die Fragen stellen: ,,Bei welchen Regelstrecken hilft sie und wann schadet sie?“ und ,,Bei welchen Sollwerten (Frequenzbereich) hilft sie und wann ist sie destruktiv?“.
Die Ungleichung (2) lässt sich für die komplexe Zahl ![]() lösen. In Abb. 3-a unten ist die zulässige Lösung
lösen. In Abb. 3-a unten ist die zulässige Lösung ![]() als Bereich in der
als Bereich in der ![]() -Ebene gezeigt (Nyquist-Plot von
-Ebene gezeigt (Nyquist-Plot von ![]() ).
).
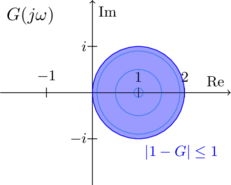
Abbildung 3-a: Lösung der Ungleichung ![]() für
für ![]() (blauer Bereich). Die Linien zeigen die Verstärkung an, die die stationäre Vorsteuerung erreicht.
(blauer Bereich). Die Linien zeigen die Verstärkung an, die die stationäre Vorsteuerung erreicht.
Zu Abb. 3-a: Wenn der Nyquist-Plot von ![]() innerhalb des lila Kreises liegt, hilft die Stationäre Vorsteuerung bei einzel-Frequenzanregungen von
innerhalb des lila Kreises liegt, hilft die Stationäre Vorsteuerung bei einzel-Frequenzanregungen von ![]() . Wieviel sie hilft zeigen die Höhenlinien als Faktor. Es sind drei Höhenlinien
. Wieviel sie hilft zeigen die Höhenlinien als Faktor. Es sind drei Höhenlinien ![]() eingezeichnet. Ein Faktor kleiner 1 reduziert den Regelfehler um eben diesen Faktor. Liegt
eingezeichnet. Ein Faktor kleiner 1 reduziert den Regelfehler um eben diesen Faktor. Liegt ![]() außerhalb des Kreises, so ist die Stationäre Vorsteuerung destruktiv.
außerhalb des Kreises, so ist die Stationäre Vorsteuerung destruktiv.
In Abb. 3-b ist diese Menge in Amplitude und Phase von ![]() umgerechnet. Da wir alle wahrscheinlich besser in Phase denken können, als im Nyquist-Plot.
umgerechnet. Da wir alle wahrscheinlich besser in Phase denken können, als im Nyquist-Plot.
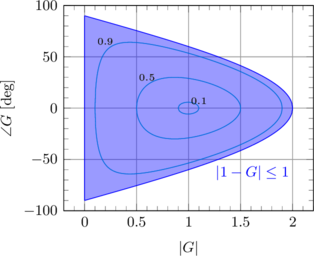
Abbildung 3-b: Lösung der Ungleichung ![]() für
für ![]() (blauer Bereich), umgerechnet in Phase und Amplitude von
(blauer Bereich), umgerechnet in Phase und Amplitude von ![]() . Die Linien zeigen die Verstärkung an, die die stationäre Vorsteuerung erreicht (kleiner 1 ist gut).
. Die Linien zeigen die Verstärkung an, die die stationäre Vorsteuerung erreicht (kleiner 1 ist gut).
Zu Abb. 3-b: Die Höhenlinien zeigen die Verbesserung der Stationären Vorsteuerung (je kleiner desto besser). Sie sind abhängig von Phase und Amplitude von ![]() . Liegt Phase oder Amplitude von
. Liegt Phase oder Amplitude von ![]() außerhalb des lila-Bereiches, dann schadet die Stationäre Vorsteuerung.
außerhalb des lila-Bereiches, dann schadet die Stationäre Vorsteuerung.
Die betragsmäßig maximal zulässige Phase ![]() kann in Abhängigkeit der erreichten Verkleinerung
kann in Abhängigkeit der erreichten Verkleinerung ![]() des Regelfehlers
des Regelfehlers ![]() angegeben werden:
angegeben werden:
![]()
Der Zusammenhang ist in Abb. 3-c dargestellt.
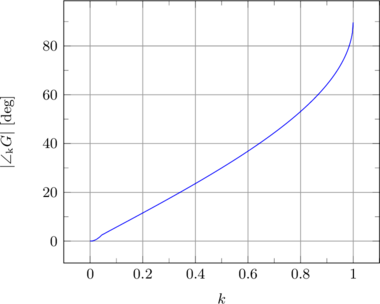
Abbildung 3-c: Maximale Phase der Strecke in Abhängigkeit der zu erreichenden Verbesserung ![]() .
.
Abb. 3-c zeigt, dass eine gute Unterdrückung (![]() klein) des Regelfehlers durch die Stationäre Vorsteuerung eine Phase der Strecke nahe 0 erfordert. Beispiel: Fordert man eine Verbesserung (Verkleinerung) des Regelfehlers um
klein) des Regelfehlers durch die Stationäre Vorsteuerung eine Phase der Strecke nahe 0 erfordert. Beispiel: Fordert man eine Verbesserung (Verkleinerung) des Regelfehlers um ![]() (
(![]() ), so findet man, dass dies eine Phase (Betrag der Phase) von maximal 45 Grad erfordert. Bei -6dB findet man 30 Grad maximale Phase. Zusätzlich muss
), so findet man, dass dies eine Phase (Betrag der Phase) von maximal 45 Grad erfordert. Bei -6dB findet man 30 Grad maximale Phase. Zusätzlich muss ![]() exakt den richtigen Wert haben, sonst ist die Verbesserung noch schlechter.
exakt den richtigen Wert haben, sonst ist die Verbesserung noch schlechter.
Fazit zu Variante 1. Wünscht man sich von der stationären Vorsteuerung eine Verkleinerung des Regelfehlers über alle Frequenzen ![]() von
von ![]() so funktioniert das nur bei einer extrem eingeschränkten Systemklasse. Die zulässige Systemklasse ist eine Unterklasse der passiven (auch ,,SPR“) Systeme. Das heißt: Stabil, minimalphasig, relativer Grad
so funktioniert das nur bei einer extrem eingeschränkten Systemklasse. Die zulässige Systemklasse ist eine Unterklasse der passiven (auch ,,SPR“) Systeme. Das heißt: Stabil, minimalphasig, relativer Grad ![]() oder
oder ![]() und eine Amplitudenbeschränkung in Abhängigkeit der Phase (s. Abb. 3-c). Darunter fallen sog. ,,PT1„ Strecken mit beliebiger Zeitkonstante. Alle anderen Systeme — also solche außerhalb der blauen Bereiche in Abb. 3-b — schaden dem Regelfehler in manchen Frequenzen.
und eine Amplitudenbeschränkung in Abhängigkeit der Phase (s. Abb. 3-c). Darunter fallen sog. ,,PT1„ Strecken mit beliebiger Zeitkonstante. Alle anderen Systeme — also solche außerhalb der blauen Bereiche in Abb. 3-b — schaden dem Regelfehler in manchen Frequenzen.
Selbst für die zulässige Systemklasse findet man eine spürbare Verkleinerung des Regelfehlers nur in den Frequenzbereichen mit sehr kleiner Phase. Bei Phasen unter -45 Grad (dies ist bei einem PT1 exakt bei -3 dB Amplitude der Fall) ist die positive Wirkung auf den Regelfehler kaum noch zu spüren.
Es liegt nun nahe zu deklarieren, dass eine Stationäre Vorsteuerung für eben diese Systemklasse (so klein sie auch sein mag, sie enthält schließlich alle PT1) zu verwenden besser ist, als nur einen Standardregler. Dem ist nicht so: Für diese Systemklasse kann ein Standardregler beliebige Regelgüte erreichen. Beispiel: Sei ![]() ein P-Regler mit beliebig hoher Verstärkung dann erreicht die Empfindlichkeitsfunktion beliebig kleine Werte (
ein P-Regler mit beliebig hoher Verstärkung dann erreicht die Empfindlichkeitsfunktion beliebig kleine Werte (![]() für
für ![]() ) mit einem komfortablem Phasenrand von mindestens 90 Grad. Es existiert also stets ein Standardregler, der eine bessere Regelgüte erreicht, als ein gegebener Standardregler mit Stationärer Vorsteuerung. Nur und ausschließlich in dem Fall, dass die gewünschte Bandbreite (ein Begriff der im Folgenden definiert wird) des geschlossenen Kreises durch Messrauschen nicht erreicht werden kann, kann eine Stationäre Vorsteuerung bei PT1 Systemen Verbesserung bringen.
) mit einem komfortablem Phasenrand von mindestens 90 Grad. Es existiert also stets ein Standardregler, der eine bessere Regelgüte erreicht, als ein gegebener Standardregler mit Stationärer Vorsteuerung. Nur und ausschließlich in dem Fall, dass die gewünschte Bandbreite (ein Begriff der im Folgenden definiert wird) des geschlossenen Kreises durch Messrauschen nicht erreicht werden kann, kann eine Stationäre Vorsteuerung bei PT1 Systemen Verbesserung bringen.
Bei allen Systemen (außer passiven (z.B. PT1)) schadet die Stationäre Vorsteuerung der Performance (nach der hier gewählten Bewertung).
Variante 2: Auswirkung auf quadratisch integralen Regelfehler (ISE, L2-Norm)
Fans der Stationären Vorsteuerung könnten jetzt sagen: ,,Moment! Es wurden ja nur alle Frequenzem einzeln untersucht! Wenn man nach dem quadratisch integralem Regelfehler beurteilt, könnte das Ergebnis ganz anders aussehen!“.
Dieser Blog-Artikel ist nun schon etwas lang geworden. Um ihn nicht ausufern zu lassen, lassen Sie mich nur kurz skizzieren, wie man dieser Aussage entgegnen könnte und was das Ergebnis ist.
Die ![]() -Norm (
-Norm (![]() ) des Regelfehlers
) des Regelfehlers ![]() ist ein oft genutztes Maß für Regelgüte. Anders als die frequenzweise Betrachtung der Empfindlichkeitsfunktion erlaubt es die
ist ein oft genutztes Maß für Regelgüte. Anders als die frequenzweise Betrachtung der Empfindlichkeitsfunktion erlaubt es die ![]() -Norm, den Zeitverlauf des Regelfehlers zu bewerten. Dieses Kriterium ist — wie auch die frequenzweise Betrachtung — nicht alleine aussagefähig.
-Norm, den Zeitverlauf des Regelfehlers zu bewerten. Dieses Kriterium ist — wie auch die frequenzweise Betrachtung — nicht alleine aussagefähig.
Der Parseval’sche Satz erlaubt es (bei stabilen Regelkreisen, von denen wir ausgehen) die ![]() -Normen des Ein- und Ausgangssignals über die
-Normen des Ein- und Ausgangssignals über die ![]() -Norm der betreffenden Übertragungsfunktion in Beziehung zu stellen. Für den hier besprochenen Fall finden wir:
-Norm der betreffenden Übertragungsfunktion in Beziehung zu stellen. Für den hier besprochenen Fall finden wir:
(3) ![]()
- Die
 -Norm der Sensitivität (Empfindlichkeitsfunktion) ist deren maximale Verstärkung über alle Frequenzen, genannt
-Norm der Sensitivität (Empfindlichkeitsfunktion) ist deren maximale Verstärkung über alle Frequenzen, genannt  .
. - Die Bandbreite (Geschwindigkeit)
 des geschlossenen Regelkreises ist die erste Frequenz bei der die Empfindlichkeitsfunktion
des geschlossenen Regelkreises ist die erste Frequenz bei der die Empfindlichkeitsfunktion  dB überschreitet.
dB überschreitet. - Die Bandbreite
 der Regelstrecke ist die letzte Frequenz, bei der
der Regelstrecke ist die letzte Frequenz, bei der  dB unterschreitet.
dB unterschreitet.
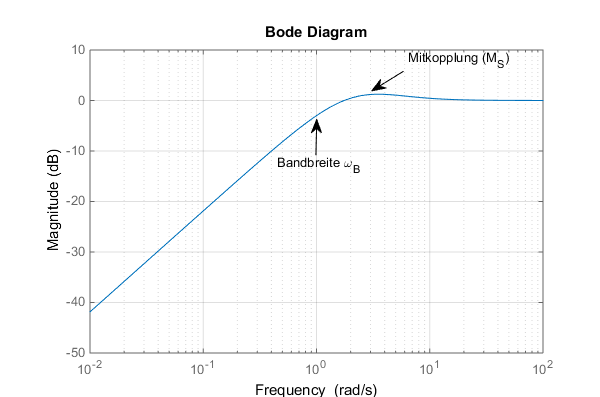
Abb. 4 zeigt einen typischen Verlauf der Sensitivität. Wir lernen aus (3):
1. Damit die Stationäre Vorsteuerung den integral quadratischen Regelfehler verkleinert, muss
im Mittkopplungsbereich des Regelkreises kleiner 1 sein.
2. Der Mittkopplungsbereich (bei
) liegt über der Bandbreite
des geschlossenen Regelkreises.
Damit wird die Wirkung der Stationären Vorsteuerung zur Geschwindigkeit des Regelkreises in Beziehung gestellt:
Die Wirkung der Stationären Vorsteuerung
muss bei Frequenzen über der Bandbreite
des Regelkreises kleiner 1 sein. Ist sie das nicht, ist sie destruktiv.
die Bandbreite
des geschlossenen Kreises durch die Stationäre Vorsteuerung limitiert ist!
Zumindest, wenn wir eine Verbesserung der Performance nach ISE Norm verlangen. Das ist eine irre wichtige Erkenntnis! Wenn man die Stationäre Vorsteuerung benutzt, so limitiert man (bei fast allen Regelstrecken) die Bandbreite des geschlossenen Kreises und damit auch die erreichbare Geschwindigkeit!!
Wir stellen fest, dass die Phase der Regelstrecke bei deren Bandbreite
innerhalb +/- 69° liegen muss, damit die Stationäre Vorsteuerung helfen kann!
Fazit für Variante 2:
Erwartet man eine Verbesserung der Performance nach der ISE Norm (integral quadratischem Regelfehler),
dann erfordert dies eine Bandbreite (Geschwindigkeit) des geschlossenen Kreises unter oder gleich der Bandbreite (Geschwindigkeit) der Geschwindigkeit der Regelstrecke!
Fazit zur Performance durch die Stationäre Vorsteuerung
Die Stationäre Vorsteuerung hilft der Performance nur dann, wenn man extrem langsame Performance will. Sobald man eine Regelstrecke durch einen Regler ,,beschleunigen“ will, dann schadet die Stationäre Vorsteuerung bei allen relevanten Fällen der Praxis!
Es gibt ein paar homöopathische Ausnahmen für PT1 Strecken. Aber die kann man auch ohne Vorsteuerung schon beliebig schnell regeln. Sobald man komplexere Strecken hat (PT2, PT3, etc.) und dämlicherweise eine Stationäre Vorsteuerung verwendet, muss man die Bandbreite des geschlossenen Kreises über schwache Regler stark limitieren.
Man erahnt nun schon, dass, wenn man eine Stationäre Vorsteuerung vorfindet, die Störunterdrückung extrem stark leidet.
Ich habe schon die ein oder andere Stationäre Vorsteuerung in Serie gefunden. Wir haben diese dann entfernt und einen anständigen Regler ausgelegt. In aller Regel haben wir eine schnellere Regelung erreicht und eine Störunterdrückung, die mindestens um Faktor 5 (also 500%) besser war. Sobald man eine Stationäre Vorsteuerung in Serie findet, weiß man: Hier ist es einfach den Serienregler so brutal zu schlagen, dass der sturste Kunde mit Wohlwollen den neuen Regler kauft.
Es ist irgendwie witzig: Der Grundgedanke der Stationären Vorsteuerung war wohl immer: ,,Sie hilft bestimmt ein bissl!“. Aber wir stellen fest: Wenn man sie verwendet, ist es als würde man der Regelung Handschellen anlegen und alles wird langsamer.
Warum merkt man das denn in Serie nicht? Nunja, ganz einfach: Weil in der Automobilindustrie immer zuerst die Stationäre Vorsteuerung angeschaltet wird und dann erst der Regler entworfen wird. Würde man es anders herum machen, würde man merken, was die Stationäre Vorsteuerung für eine schlechte Idee ist.
Im nächsten und letzten Teil stellen wir die verbleibende Frage:
Wenn man die Stationäre Vorsteuerung frei bedaten kann, (also nicht ![]() für
für ![]() will) welcher Wert wäre gut?
will) welcher Wert wäre gut?