Wir haben im zweiten Teil dieser Serie gesehen, dass die schlechte Modellgüte bei der Systemidentifikation mit Sprungantworten auf das ungünstige Amplitudenspektrum der Sprungfunktion zurückgeführt werden kann. Daher stellt sich nun die Frage, wie ein geeignetes Amplitudenspektrum aussieht und mit welchem Zeitsignal sich dieses darstellen lässt. Hierzu ist es hilfreich, sich etwas genauer mit der Frequenzgangschätzung zu beschäftigen, da wir ja wissen, dass der Frequenzgang – im Gegensatz zur Sprungantwort – der entscheidende Faktor für die genaue Modellierung des Systemverhaltens ist
Die Frequenzgangschätzung
Es existieren eine Reihe von unterschiedlichen Methoden zur Frequenzgangschätzung, wobei die am häufigsten Verwendete die sogenannte H1-Methode ist. Diese verbirgt sich, in leicht abgewandelter Form, auch hinter diversen Befehlen der System Identification Toolbox von Matlab®.
Deren Eigenschaften sind (bei einer ausreichenden Länge der Messdaten) bekannt und leicht zu begreifen. Die zentrale Aussage liefert folgende Gleichung für die Varianz der Schätzung des Frequenzgangs an der Frequenz 
,
Dabei bezeichnen 
| die Amplitudendichte des Anregungssignals, wie wir sie bereits bei der Analyse der Sprungfunktion verwendet haben, und 
die Varianz des Messrauschens. Letzteres wurde hier als bandbegrenztes weißes Rauschen über den relevanten Frequenzbereich 
angenommen. Weiter gehen wir davon aus, dass die Messung mit demselben Anregungssignal 
mal wiederholt wird und keine weiteren Störquellen vorliegen.
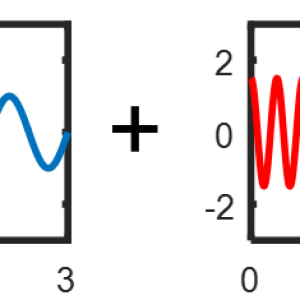
Fordert man nun eine über den betrachteten Frequenzbereich konstante, ausreichend kleine Varianz 
, so ergibt sich damit unmittelbar die Forderung nach einer über der Frequenz konstanten Amplitudendichte. Die Sprungfunktion ist davon – wie wir in Teil 2 gesehen haben – weit entfernt. Aber schon mit bewährten Standard-Signalen, wie dem Gleit- oder Multisinus, kommt man an dieses Ideal sehr nahe heran. Eine Stellgrößenbeschränkung des Zeitsignals kann dabei problemlos eingehalten werden. Die folgenden Bilder zeigen jeweils ein Beispiel für den Gleit- und Multisinus für eine Anregung bis 250Hz bei einer Stellgrößenbeschränkung von eins.
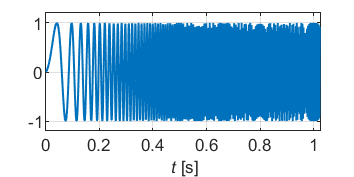
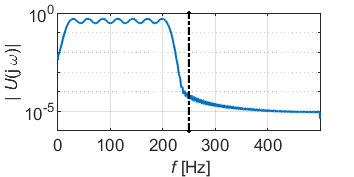
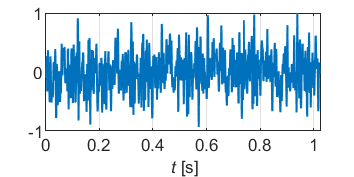
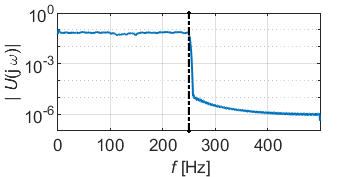
Wir gehen nun im Weiteren davon aus, dass man im relevanten Frequenzbereich eine ideal konstante Amplitudendichte erzeugen kann und fragen uns, um wieviel genauer damit die Frequenzgangschätzung im Vergleich zur Sprungfunktion werden kann.
Unter geeigneten experimentellen Bedingungen ist die H1-Methode biasfrei, d.h. der Gesamtfehler der Schätzung entstammt ausschließlich der in Gleichung (3) gegebenen Varianz aufgrund von Messrauschen. Als Fehlermaß des geschätzten Frequenzgangs wollen wir zwei Standardabweichungen festlegen, d.h.
Damit ergibt sich unmittelbar das Fehlerverhältnis von Sprunganregung zu idealer Anregung zu
.
Für das System aus dem Motivationsbeispiel von Teil 1 beträgt die Dauer der Impulsantwort ca. 6 Sekunden. Mit einem Gleitsinus der Amplitude eins und dieser Dauer lässt sich in sehr guter Näherung eine konstante Amplitudendichte 
im Frequenzbereich zwischen 
rad/s und 
rad/s darstellen. Der Verlauf von 
der Sprungfunktion mit der gleichen Amplitude und Dauer wie beim Gleitsinus entspricht nun nicht mehr exakt dem bisher betrachteten hyperbelförmigen Verlauf, da eine endliche Zeitdauer betrachtet wird. Die beiden Amplitudendichten und das Fehlerverhältnis sind in den folgenden Bildern dargestellt.
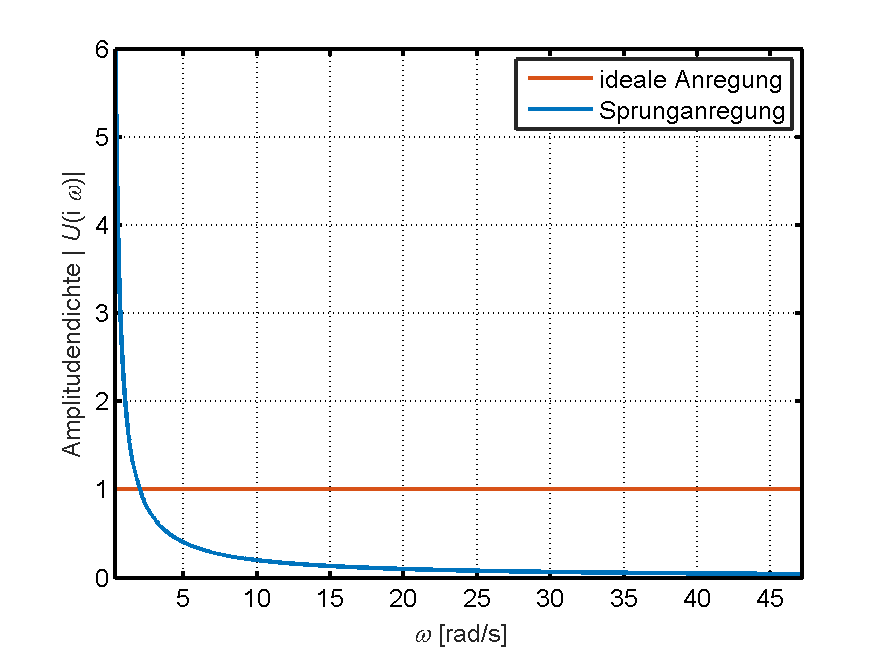
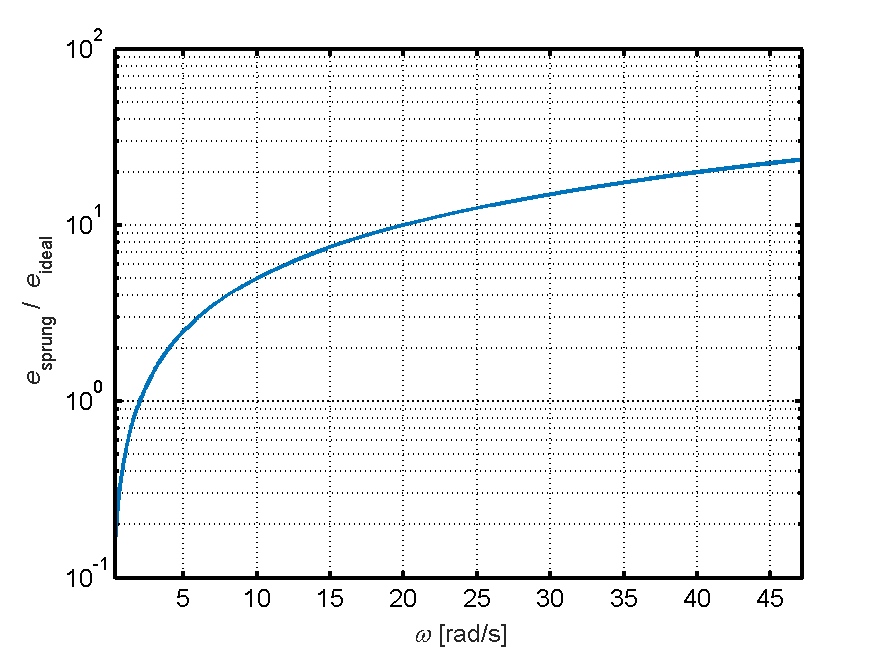
Bereits ab einer Frequenz von 2.0 rad/s liegt das Fehlerverhältnis über eins und steigt bis zum oberen Ende des relevanten Frequenzbereichs bis auf 24 an. Wie in Gleichung (4) ersichtlich, geht die Anzahl der Messwiederholungen mit der Wurzel in die Fehlerberechnung ein.
Das bedeutet, dass man 24² = 576-mal die Messung der Sprungantwort wiederholen müsste, um bei
die gleiche Güte zu erreichen, wie bei einer einzigen Messung mit dem Gleitsinus!
die gleiche Güte zu erreichen, wie bei einer einzigen Messung mit dem Gleitsinus!Wir wollen zum Abschluss den Einfluss der beiden verschiedenen Anregungen noch in Form von Bode-Diagrammen darstellen, da diese Darstellung besonders intuitiv ist. Dazu tragen wir den Betrag des Frequenzgangs – den sog. Amplitudengang – des wahren Systems aus unserem Motivationsbeispiel zusammen mit den jeweiligen Fehlerabschätzungen über der Frequenz auf. Es gilt hierbei folgender einfacher Zusammenhang zwischen der Standardabweichung des Frequenzgangs 
und der des zugehörigen Betrags 
:
.
Die nachfolgenden Bilder zeigen für die ideale und sprungförmige Anregung jeweils das wahre System, dessen Fehlerabschätzung (in Form von zwei Standardabweichungen), und das aus der Sprungantwort in Teil 1 bestimmte PT1-Modell. Es wurde jeweils von M = 10 Experimenten ausgegangen. Die notwendige Gesamtmesszeit wäre damit bei beiden Anregungen identisch, die erreichbare Modellgüte jedoch wesentlich unterschiedlich!
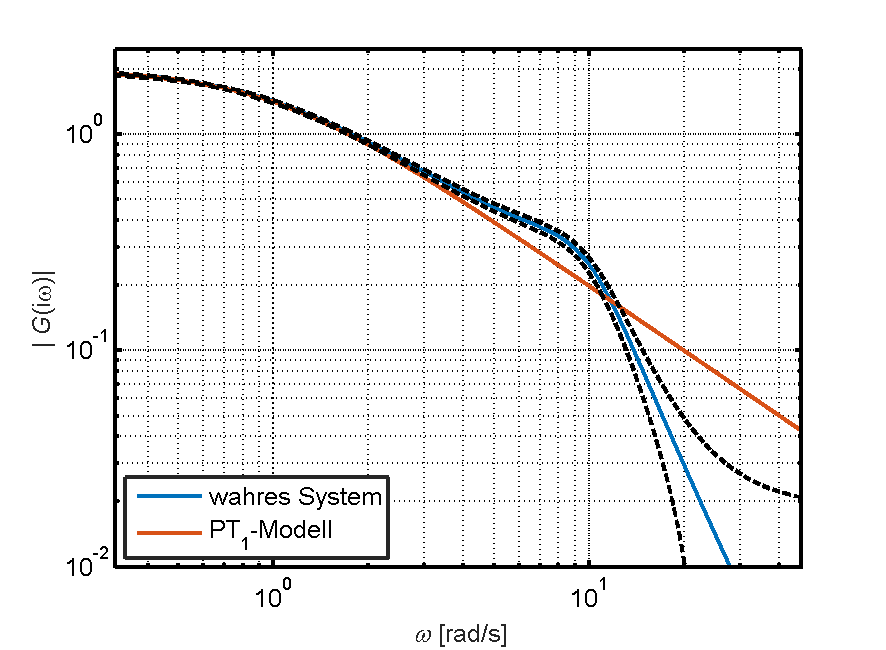
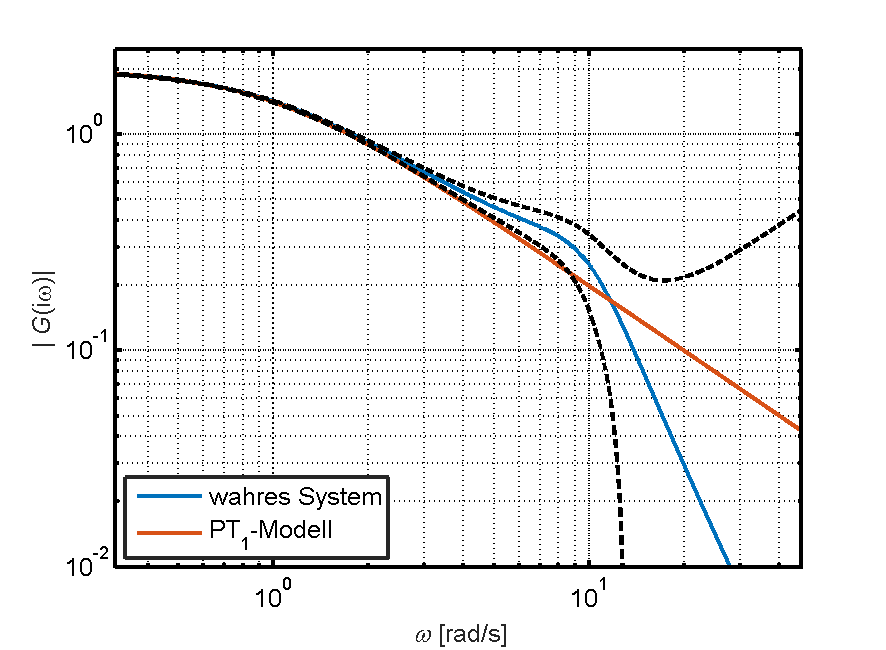
Die ideale Anregung führt zu deutlich kleineren Fehlerabschätzungen. Das PT1-Modell liegt dabei weit außerhalb der Fehlerabschätzung und ist somit klar als invalide gekennzeichnet. Die erreichbare Schätzgenauigkeit bei Sprunganregung ist so schlecht, dass nicht erkennbar ist, dass die Systemdynamik nie durch ein PT1-Modell abgebildet werden kann.
Mit einer methodisch korrekten Frequenzgangschätzung, inklusive Fehlerabschätzung, lässt sich also im Vornherein feststellen, dass ein PT1-Modell ungeeignet ist, um das reale Systemverhalten abzubilden. Die böse Überraschung kommt also nicht erst, wenn man, basierend auf dem schlechten Modell, einen Regler entworfen hat und dieser dann – wider erwarten – am realen System nicht funktioniert.
Darüber hinaus lässt sich der Fehler in der Modellbildung durch eine geeignete Wahl des Anregungssignals, wie oben gesehen, um mehrere Zehnerpotenzen verkleinern!
Mit ausreichend Fachwissen und den richtigen Kniffen für die Praxis haben Sie das Werkzeug in der Hand, um zielsicher Modelle zu identifizieren, die Sie für Ihre Anwendungen in den Bereichen Reglerentwuf, Diagnose und Prädiktion brauchen.
Alles, was Sie hierzu benötigen, vermitteln wir in unserem Seminar:
Sehr geehrte Damen und Herren,
Ihre Artikelserie ist sehr interessnt lässt aber Fragen offen:
1. Wenn es sich nicht um eine PT1 Strecke handelt um was handelt es sich dann? Oder anders gefragt: Wie kommt man mit Ihrer Erkenntnis letztendlich zu einem Regler?
2. Wie läuft das Ganze in der Praxis ab? Ich habe z.B. eine Induktionsheizung, die von einem Regler per PWM und SSR angesteuert wird. Wo schließe ich da wie einen Sweep-Generator an? Und auf welche Werte stelle ich diesen dann ein? Und wie komme ich dann zu den PID-Parametern für meinen Regler?
3. In welchen Fällen reicht eine Sprungantwort zur Charakterisierung einer Regelstrecke und in welchen Fällen empfiehlt sich Ihr „Sinus“-Verfahren?
Vielen Dank für Ihre Antwort.
Mit freundlichen Grüßen
Jürgen Broß
Hallo Herr Broß,
1. Ihre erste Frage habe ich nicht ganz verstanden. Es könnte im Prinzip jede Art der Strecke sein. Im Arbeitspunkt (also, bei Ihnen wahrscheinlich um einen Temperaturbereich herum) sind fast alles Strecken im Wesentlichen linear (Ausnahmen zu der Aussage gibt es, sind aber kaum zu erwarten). Bei linearen Strecken haben wir in der Praxis meist eine kleine Totzeit und „irgendeine“ Dynamik.
Wie man zu einem Regler kommt, ist eine sehr gute Frage. Wir unterstützen hier gerne – das ist ja unser Angebot: Wir unterstützen genau bei diesen Fragen. Wir sind gerne für Sie erreichbar.
2. Grundsätzlich steuern sie die „möglichst weit außen“ gelegenen Steller an. Bei Ihnen wäre dies wohl das PWM. Die Idee ist, dass die Dynamik aller innenliegender Umsetzungen der außen anliegenden Steuerung mit identifiziert werden.
3. Grundsätzlich sind Sprungantworten zu vermeiden. Wir haben schon viele Fehleinstellungen von Reglern gesehen, die auf Modellbildung mittels Sprungantwort zurückzuführen sind. Wenn Sprünge das einzige sind, das Sie aufbringen können gibt es nur noch den „Windsurfer Approach“ – welcher iterativ über Reglerentwürfe funktioniert. Dazu benötigen Sie ein Reglerentwurfsverfahren. Auch hier: Wir unterstützen gerne.
Beste Grüße,
Dieter
Hallo Dieter,
vielen Dank für deine Antwort.
Zu 1: Die Frage bezog sich auf das gegebene Beispiel im Kapitel „Ein Motivationsbeispiel“. Laut Sprungantwort wäre es eine PT1-Strecke, in Wirklichkeit war es aber eine ???-Strecke.
Zu 2: Verstehe ich das richtig: Ich müsste mit einem Sweep das Puls-Pausen-Verhältnis der PWM variieren?
Zu 3: Das Problem ist der Unterschied zwischen Theorie und Praxis. Ich habe z. B. das Problem, dass auf einer gut 20 Jahre alten Anlage ein Regler ersetzt werden soll. Der originale Regler ist ein Zweipunktregler, der aber eine firmenspezifische Parametrierung aufweist. Dafür gibt es keine Unterlagen mehr, d.h. eine einfache Kopie der Reglerparameter ist nicht möglich (das wurde schon versucht und man ist damit kläglich gescheitert). Nun soll dieser Regler durch einen PID-Regler ersetzt werden. Jeweils 3 Kanäle regeln 3 Heizzonen einer Galette. Die Heizung arbeitet induktiv, ist also relativ schnell (im Vergleich zu Widerstandsheizungen aber langsam im Vergleich zu Lampenheizungen). In jeder Heizzone gibt es einen PT2000, der die Ist-Temperatur erfasst und dessen Daten wegen der Drehbewegung der Galette per Infrarot nach außen übertragen werden. Angesteuert wird die Heizung jeweils per PWM über SSR. Hinzu kommt: Die Anlage steht in Ägypten (und wir sind in D) und wegen des Alters gibt es auch in unserem Versuchslabor keinen auch nur annährend ähnlichen Aufbau, an dem Messungen durchgeführt werden könnten. Der PID-Regler ist vor Ort, der Kunde hat Zugriff auf die Reglerparameter P, I und D. Wie würdest du dieses Problem unter den gegebenen Bedingungen angehen?
Viele Grüße
Jürgen
Hallo Herr Broß,
Sie können uns jederzeit für detaillierte Unterstützung hier erreichen.
Zu Ihren Fragen:
1. Die Strecke selbst kam vom Blog-Author, der bei uns der Spezialist für Systemidentifikation ist. Typischerwise nimmt man für solche Beispiele einen dominanten PT1 Teil und einen oder mehrere schnelle weitere PT1 oder PTx. Die Idee hinter dem Beispiel ist, dass etwas wie ein PT1 aussehen kann, aber ein Reglerentwurf mit einer solchen falsch identifizierten Strecke zu schlechten Ergebnissen führt.
2. JA, zum Beispiel ein Sinus-Sweep. Es gibt viele Anregungen, die reichhaltig in den Frequenzen (bis zu einer zu definierenden Maximalfrequenz) sind. Ein Sweep, ein PBRS, Rauschen, etc. Was für Sie gut passt und leicht umsetzbar ist müsste man für Ihren Anwendungsfall besprechen.
3. Ich verstehe Ihr Problem. Die Herangehensweise ist hier mit vielen weiteren Details zu besprechen. Was ist Ihre Zielgeschwindigkeit, benötigen Sie eine starke Störunterdrückung, was ist die Verhaltensvarianz der Strecke (z.B. Umgebungsbedingungen). Wie „gut“ müssen Sie eigentlich werden? Müssen Sie an die machbaren Grenzen gehen oder reicht „irgendwie ok“ (also langsamer als möglich)? Welche Eingänge können Sie bei einer so alten Strecke überhaupt programmieren? Vielleicht geht ein Sinus-Sweep ja nicht. Dann müsste man iterativ (Windsurfer Approach) Regler entwerfen via (schlechten) Sprungantworten und sich systematisch (!) (also nicht probieren, weil das bestimmt schon erfolglos geschehen ist) einer Lösung nähern. Ein sehr einfaches Reglerentwurfsverfahren könnte IMC sein (welches eine gute ÜBersetzung in PID Parameter hat).
Ich kann Ihnen an dieser Stelle gerne Unterstützung anbieten – Genau das ist ja unser Angebot an Sie und die Industrie. Gerne können Sie uns kontaktieren.