Blog

Systemidentifikation mit Sprungantworten – Es kann einfach nicht funktionieren (Teil 2: Die Sprunganregung)

Dies ist der zweite in einer Serie von drei Beiträgen zum Thema Systemidentifikation mit Sprungantworten. Teil 1 verdeutlicht die Relevanz anhand eines Beispiels und wiederholt das notwendige Wissen zu LTI Systemen. Hier kommen wir nun zur zentralen Frage zurück: Warum sollte man überhaupt eine Systemidentifikation mit Sprungantworten durchführen wollen?

Drei schlechte Gründe für die Verwendung von Sprungantworten

Ich werde nun der Reihe nach auf die von mir am häufigsten gehörten Gründe für die Verwendung von Sprungantworten eingehen und jeweils aufzeigen, warum diese sämtlich irreführend sind.

„Der Frequenzgang ist durch die Sprungantwort bestimmt.“

Ja, das stimmt natürlich. Aus der Grundlagenvorlesung Regelungstechnik wissen wir noch, dass zwischen der Sprungantwort h(t) und dem Frequenzgang G(i\omega) folgender Zusammenhang gilt:

G(i\omega) = \mathcal F\dfrac{\mathrm dh(t)}{\mathrm dt}

Der Frequenzgang ist also die Fourier-Transformierte der zeitlichen Ableitung der Sprungantwort. Aber diese Gleichung ist nur ein Spezialfall der allgemeinen Definition, die besagt, dass der Frequenzgang gegeben ist durch das Verhältnis der Fourier-Transformierten von Aus- zu Eingangssignal:

G(i\omega) = \dfrac{\mathcal F (y(t))}{\mathcal F (u(t))} \qquad (1)

Man kann den Frequenzgang aus jedem Ein-Ausgangspaar bestimmen, welches Fourier-transformierbar ist.

Die Tatsache, dass die Fourier-Transformierte der Ableitung der Sprungfunktion gleich eins ist und daher nicht berechnet werden muss, ist kein Argument. Unserem PC ist es völlig egal ist, ob er ein oder zwei Signale transformieren muss.

„Der Sprung enthält unendlich viele Frequenzen.“

Ja, auch das ist richtig. Und auch das ist eine Binsenweisheit. Jedes Signal, welches wir praktisch verarbeiten können, hat eine endliche Dauer und ist damit zeitlich beschränkt. Und kein Signal, welches zeitlich beschränkt ist, ist in seinem Frequenzband beschränkt. Das ist ein zentraler Grundsatz der Signalverarbeitung. Und wenn ein Signal nicht spektral begrenzt ist, dann enthält es auch unendlich viele Frequenzen, also:

Jedes praktische Signal enthält unendlich viele Frequenzen.

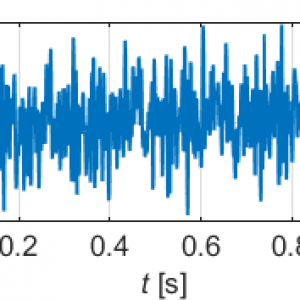
In Ihnen mag sich gerade gedanklicher Widerstand formieren. Wahrscheinlich überlegen Sie: „Aber was ist, wenn ein Signal einfach nur ein Sinussignal ist?“. Nun ja, Sie werden sicherlich nur einen zeitlich begrenzten Ausschnitt des Sinussignals betrachten. Wenn Sie ein System mit einem Sinussignal anregen, dann werden Sie dieses zu bestimmten Zeitpunkten ein- und ausschalten. Wird dieser zeitlich begrenzte Abschnitt einer Spektralanalyse unterworfen, so multiplizieren Sie faktisch vor der Analyse das ideale, unendlich andauernde Sinussignal mit einem Rechteckfenster, welches das betrachtete Zeitfenster repräsentiert. Außerhalb des Fensters wird dem Signal der Wert null zugewiesen. Das verändert das Spektrum und es kommt zum sogenannten Leakage-Effekt, der den Frequenzinhalt über die komplette Frequenzachse „verschmiert“, wie hier dargestellt:

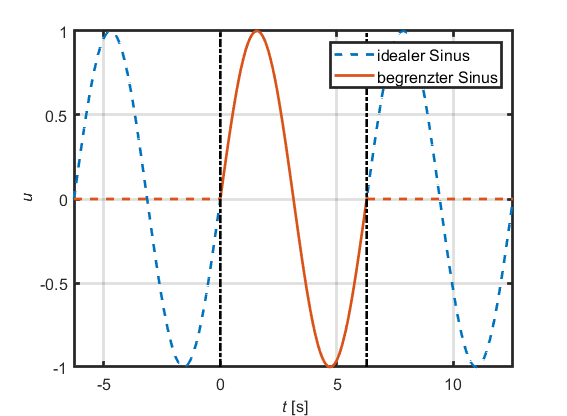
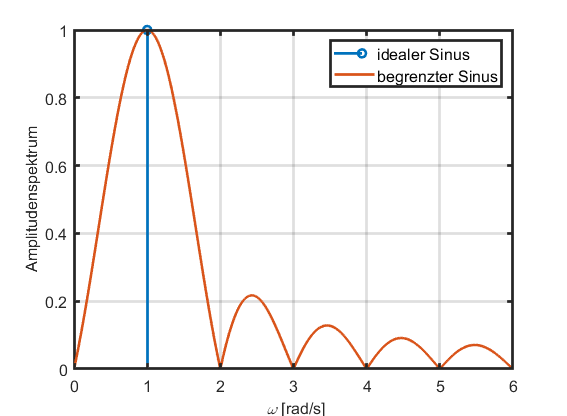
Zeitsignale von zeitlich unbegrenzter und gefensterter Sinusfunktion
Amplitudenspektrum von zeitlich unbegrenztem und gefenstertem Sinussignal

Bei der Verarbeitung von zeitdiskreten Signalen ist man bestrebt, diesen Effekt möglichst unsichtbar zu machen, indem man die Frequenzstützstellen in die Nullstellen des Spektrums legt. Aber dies sind zusätzliche Effekte der zeitdiskreten Signalverarbeitung. Wir bleiben bei der vertrauten zeitkontinuierlichen Betrachtungsweise.

„Aber der Sprung enthält alle Frequenzen.“

Auch diese Aussage ist technisch korrekt, kann aber schon mit dem wenigen von uns bisher verwendeten theoretischen Wissen als irrelevant entlarvt werden. Wie wir an obigem Beispiel gesehen haben, tauchen selbst im Spektrum eines Ausschnitts einer reinen Sinuswelle alle Frequenzen auf, bis auf abzählbar viele. Da uns für die Praxis immer nur ein endlicher Frequenzbereich interessiert, heißt das, dass nur wenige isolierte Punkte im Frequenzspektrum fehlen, also exakt null sind. Mathematisch gesprochen deckt somit jedes zeitlich begrenzte Signal das komplette Spektrum ab, bis auf eine Menge vom Maß null. Also ließe sich – unter Vernachlässigung sämtlicher Randbedingungen der Praxis – mit jedem Anregungssignal der Frequenzgang bestimmen, bis auf einen verschwindend geringen Anteil:

Jedes praktische Signal deckt das komplette Frequenzspektrum ab.

Und trotzdem hat wohl noch niemand den kompletten Frequenzgang eines realen Systems mit einer einzelnen Sinusschwingung bestimmen können , da man für eine Systemidentifikation weitere wichtige Aspekte, wie Signalabtastung, Messrauschen und Nichtlinearitäten berücksichtigen muss. Aber ist es nicht trotzdem erstaunlich?

Zwischenfazit: Obwohl wir uns auf einem idealisierten Lehrbuchniveau bewegen – und bisher sämtliche in der Praxis wichtigen Aspekte außer Acht gelassen haben – sagt uns die Theorie bereits jetzt, dass keiner der häufig genannten Gründe für die Systemidentifikation mit Sprungantworten stichhaltig ist.


Nach dem vorherigen Abschnitt ist es nun offensichtlich, dass es nicht nur darauf ankommt, welche Frequenzen in einem Anregungssignal enthalten sind, sondern auch, wie groß deren Amplituden sind. Also schauen wir uns das mit Hilfe der Spektralanalyse für die Sprungfunktion der Amplitude eins an.

Die spektralen Eigenschaften der Sprungfunktion

Die Amplitudendichte der Sprungfunktion (also das einseitige Amplitudenspektrum der Fourier-Transformierten) zeigt einen hyperbolischen Verlauf (bei linearer Achsenskalierung), bzw. einen linearen Verlauf (bei doppelt-logarithmischer Darstellung):

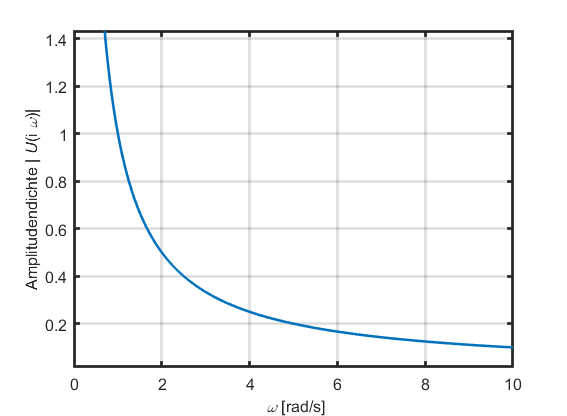
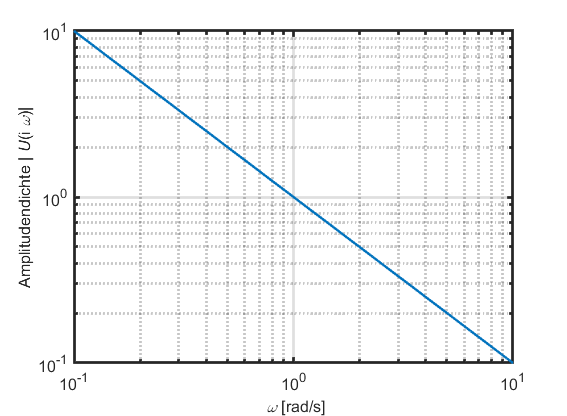
Amplitudendichte der Sprungfunktion (lineare Achsenskalierung)
Amplitudendichte der Sprungfunktion (doppelt-logarithmische Achsenskalierung)

Die obigen Darstellungen liefern uns folgende Informationen:

  • Bei der Frequenz \omega= 1 entspricht der Wert der Amplitudendichte der Sprunghöhe (in diesem Beispiel eins).
  • Je höher die Frequenz, desto geringer ist deren Anregung am zu identifizierenden System.
  • Die Frequenz null, also die stationäre Systemantwort, würde mit einer unendlich hohen Signalenergie angeregt werden, wenn der Sprung tatsächlich über einen unendlich großen Zeitraum anläge. Das tut er in der Praxis natürlich nicht, aber nichtsdestotrotz können wir ausgehend von dieser einfachen theoretischen Betrachtung wichtige Erkenntnisse gewinnen.

Wie in Gleichung (1) angegeben, bestimmt sich der Frequenzgang aus dem Verhältnis der Fourier-Transformierten von Aus- zu Eingangssignal. Die Sprungfunktion ist streng genommen nicht Fourier-transformierbar, was sich darin äußert, dass deren Spektrum bei der Frequenz null nicht endlich ist. Für die weitere Betrachtung ist dies aber unerheblich.

Durch Umstellen ergibt sich für das Spektrum des Ausgangssignals

|Y(i\omega)| = |G(i\omega)| |U(i\omega)|, \qquad (2)

falls man das Ausgangssignal fehlerfrei, d.h. vor Allem ohne Rauscheinflüsse, messen könnte. Den Verlauf von |U(i\omega)| können wir in obigem Bild ablesen. Den Verlauf von |G(i\omega)| kennen wir nicht, da wir ja genau diesen bestimmen wollen. Jedoch können folgende allgemein gültige Angaben gemacht werden:
Um das Übertragungsverhalten des betrachteten Systems identifizieren zu können, müssen wir dessen Frequenzgang im relevanten Frequenzbereich bestimmen. Dieser Bereich ist nach oben begrenzt durch eine höchste relevante Frequenz, da alle realen Systeme Tiefpass-Charakter besitzen. Wäre dem nicht so, hätte man also bei unendlich hoher Frequenz noch eine endliche Signalverstärkung, so wäre dies nur mit einer unendlich hohen Leistung zu bewerkstelligen . Nach unten ist der relevante Frequenzbereich durch eine Frequenz gekennzeichnet, welche deutlich unterhalb der der ersten Pol- bzw. Nullstelle liegt. Im Extremfall bedeutet das die Frequenz null (stationäre Systemantwort). Wir wollen den relevanten Frequenzbereich also mit dem Frequenzintervall [\omega_{min}, \omega_{max}] kennzeichnen.

Die Frequenz \omega_{max} liegt somit naturgemäß ein stückweit oberhalb des Kehrwertes der schnellsten Zeitkonstante des Systems. Ab hier gehen die Signalverstärkung und damit auch die Ausgangsamplitude des Systems bei nahezu konstanter Phasenverschiebung gegen null. Dies geschieht bei einer Sprunganregung besonders „schnell“, d.h. der Abfall des Ausgangsspektrums über der Frequenz ist besonders steil, weil ja auch die Eingangsamplitude über der Frequenz deutlich abnimmt. Durch die Multiplikation des Frequenzgangs mit dem Eingangsspektrum, siehe Gl. (2), erhöht sich der Amplitudenabfall des Ausgangs, wie in folgendem Bild dargestellt ist.

Zusammenspiel von Amplitudenspektrum des Anregungssignals und Streckenverstärkung

In der Praxis führt dieser Effekt oft dazu, dass die Signalamplitude des ungestörten Ausgangssignals schon deutlich unterhalb von \omega_{max} unter die der Störung fällt. Damit geht das Nutzsignal sprichwörtlich im Rauschen unter und kann (theoretisch) nur noch durch sehr lange Messzeiten herausgefiltert werden – und auch nur dann, wenn die Störung ein idealer stochastischer Prozess wäre!

Sie erinnern sich noch an unser Motivationsbeispiel aus Teil 1? Dann verstehen Sie jetzt, was dort passiert ist: Das Messsignal der Sprungantwort war etwas verrauscht (was in der Realität immer der Fall ist) und es konnten daraus nur die niederfrequenten Anteile der Systemdynamik bestimmt werden. Für das Übertragungsverhalten bedeutende, hochfrequente Anteile waren im Modell falsch widergegeben und wurden daher beim Reglerentwurf inkorrekt berücksichtigt – mit dem gezeigten katastrophalen Resultat.
Aber selbst für den unrealistischen Fall, dass man das ungestörte Ausgangssignal messen könnte, wäre die Sprunganregung denkbar ungünstig. In folgendem Bild sind die Sprungantworten des ungestörten Systems und des Modells zu sehen.

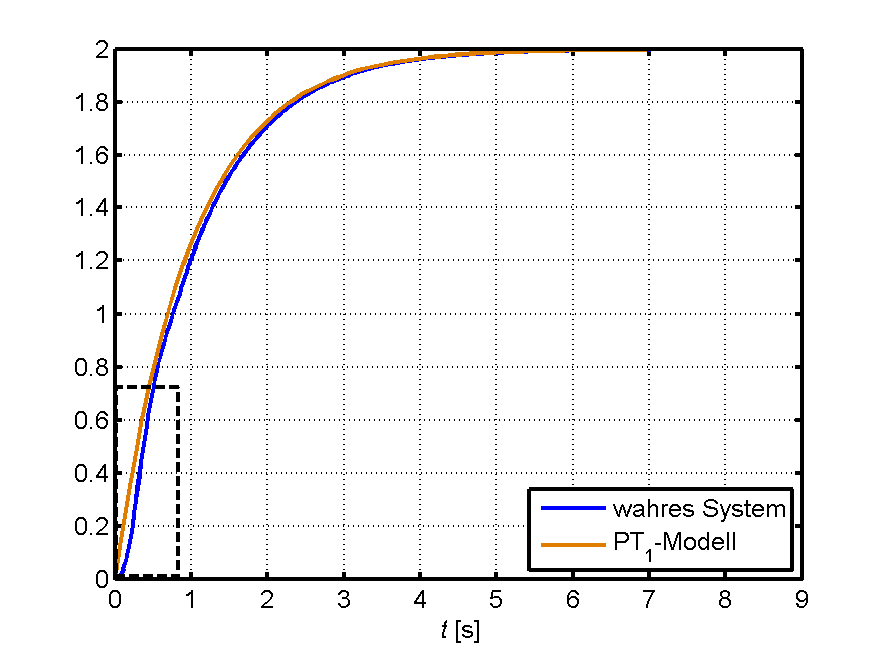
Sprungantworten des wahren Systems (ohne Messrauschen) und des Modells

Man könnte meinen:

„Super, die Sprungantwort des Modells passt sehr gut! Dann habe ich auch einen kleinen Modellfehler“

Das stimmt so nicht. Denn auch wenn keine Störung vorliegt, werden die hochfrequenten Dynamikanteile des Systems nur gering angeregt und sind damit unter Umständen selbst im ungestörten Ausgangssignal kaum sichtbar, wie hier innerhalb der ersten 0,5s nach dem Sprung.

Zwei Systeme können bei sehr ähnlicher Sprungantwort stark unterschiedliche Frequenzgänge aufweisen.

Also, selbst bei unrealistisch günstigen Annahmen ist die Sprunganregung im Allgemeinen keine gute Idee!

„Aber wie kann man es besser machen? Und wieviel besser kann man werden?“

Auch diese Fragen können mit etwas Fachwissen beantwortet werden. Das ist Thema des nächsten und letzten Beitrags.

Schlagwörter: , , ,

Schreiben Sie einen Kommentar