Blog

Drei Gründe gegen die Stationäre Vorsteuerung (Teil 1: Überschwingen)

Vorwort

Leider wird die Theorie in der Umsetzung oft beiseite gelegt. Wir kennen das alle. Zeitdruck, Kundendruck und man setzt den ersten Gedanken ,,husch husch“ um, den man hat oder übernimmt was andere vorgelegt haben, ohne es kritisch zu bewerten. Es funktioniert dann manchmal nicht so, wie erwartet und man fängt an zu basteln (Balkone/Pflaster). Das alles obwohl fundierte Kenntnisse mit den richtigen Werkzeugen schnellere und robustere Ergebnisse produzieren. Die „Stationäre Vorsteuerung“, um welche es im Folgenden geht, ist solch ein Beispiel aus der Industrie, welches diesem Muster folgt.

Nichts ist so gut, wie eine gute Theorie. Kein gezieltes Handeln ohne Theorie und die Probleme sind deutlich kleiner.

Diese dreiteilige Serie von Blog-Artikeln bewertet die Stationäre Vorsteuerung, die eine Erfindung der Industrie ist. In diesem ersten Teil schauen wir, welche (schlechte) Auswirkung sie auf die Sprungantwort hat.

Vor einigen Jahren ist mir die Stationäre Vorsteuerung beim Re-Engineering eines vorhandenen Serien-Reglers aufgefallen. Mir war völlig unklar, warum man so eine Struktur wählen würde. Insbesondere deshalb, weil sie und der I-Anteil des Reglers dieselbe Aufgabe erfüllen (mehr dazu weiter unten). Ich habe nachgefragt, was der Gedanke dabei ist und wie man damit umgeht. Die Antworten waren, frei nach Erinnerung:

,,Die Stationäre Vorsteuerung sorgt für Geschwindigkeit. Und wenn man keine dynamische Vorsteuerung entwerfen will, dann hilft sie schon sehr. Wie will man den sonst für Performance sorgen?“

Zur Applikation:

,,Man stellt das System von Hand solange konstant ein, bis der Sollwert stationär erreicht wird, die so gefundene Stellgröße trage ich dann ein“. Oder alternativ ,,Ich nutze einen I-Regler ohne Vorsteuerung und warte bis der Sollwert stationär erreicht ist und stell den Wert des Integrators dann als Vorsteuerungsfaktor ein“

Meine persönliche Meinung aus welchen Überlegungen die Stationäre Vorsteuerung entstanden sein mag, ist:

Bei nichtlinearen Systemen, die hauptsächlich eine statische Nichtlinearität haben, will man mit der Stationären Vorsteuerung eine Art Linearisierung durchführen. Das heißt, man versucht damit den Arbeitspunkt auf den stationär richtigen Wert zu legen. Der Gedanke zu Arbeitspunkten ist richtig – die Realisierung via Vorsteuerung jedoch fragwürdig.

Falls für Sie, lieber Leser, diese Idee neu ist, lesen Sie am besten nicht weiter. Merken Sie sich nur eins: Machen Sie das nicht! Nie. Finger weg von der stationären Vorsteuerung!

In den kommenden Wochen werde ich, beginnend mit diesem Blog-Artikel, die Stationäre Vorsteuerung bewerten. Wir beginnen hier mit einer Eigenschaft der Stationären Vorsteuerung, die unausweichlich schlecht ist. Doch zuvor müssen wir besprechen, was die „Stationäre Vorsteuerung“ eigentlich ist.

Die Stationäre Vorsteuerung

Die Stationäre Vorsteuerung stellt das Produkt aus Sollwert und inverser stationärer Verstärkung der Regelstrecke als Stellgröße additiv zum Regelausgang. Oder anders gesagt, sie sorgt dafür, dass die Regelstrecke ohne Regler dem Sollwert (stationär) folgt.

Malen wir mal auf, was passiert:

Rendered by QuickLaTeX.com

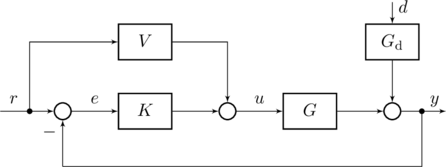
Abbildung 1: Standardregler mit Vorsteuerung und Störeingriff

Der betrachtete Regelkreis ist in Abb. 1 dargestellt. Die Signale sind wie üblich: r der Sollwert, e der Regelfehler, u das Stellsignal und d ein Störeingriff. Die Blöcke sind: K der Regler, V die Vorsteuerung, G die Regelstrecke und G\sr{d} das Störverhalten.

Die Stationäre Vorsteuerung ist definiert als die Inverse der stationären Verstärkung der Regelstrecke

(1)   \begin{equation*} V = \left[ G(s \rightarrow 0)\right]^{-1} \end{equation*}

Systemklasse. Wir gehen, der Einfachheit halber, vom SISO Fall aus. Gleichung (1) ist die Übersetzung des Vorgehens aus der Praxis in eine Gleichung. Diese Gleichung hat Schwächen, da G(s=0) bei Polen auf der imaginären Achse nicht das stationäre Verhalten wiedergibt. Regelstrecken G mit Polen auf der imaginären Achse müssen von den folgenden Untersuchungen ausgenommen werden. Dies gilt auch für rein integrierende Strecken, die häufig in der Praxis vorkommen. Bei diesen könnte man auch argumentieren, dass offensichtlich keine Vorsteuerung verwendet werden würde (da \abs G \rightarrow \infty für s\rightarrow 0 und daher V=0). Instabile Strecken hingegen können im Folgenden problemlos mit betrachtet werden.

Übertragungsfunktionen im Regelkreis. Das Verhalten des Ausgangs y und des Regelfehlers e=r-y kann in Abhängigkeit der anderen Signale berechnet werden zu

(2)   \begin{align*} y &= (1+ G K)^{-1} \left[\, G (K+V) r +G\sr{d} d\, \right] \\ e &= (1+ G K)^{-1} \left[(1-G V) r - G\sr{d} d\right]. \end{align*}

Vereinfachter allgemeiner Fall. Es wird gezeigt, dass ohne Beschränkung der Allgemeinheit, für unsere Untersuchungen, eine stationäre Verstärkung der Strecke von eins angenommen werden darf.

In den Gleichungen (2) wird ersichtlich, dass die Regelstrecke G nur in Verkettung mit entweder dem Regler K oder der Vorsteuerung V vorkommt. Daraus kann geschlossen werden, dass die stationäre Verstärkung G(s=0) immer von K oder V kompensiert werden kann.

Ohne Beschränkung der Allgemeinheit wird im Folgenden angenommen, dass die stationäre Verstärkung der Strecke eins ist (G(s=0)=1). Daraus folgt, dass die Stationäre Vorsteuerung (in diesem Fall) ebenso eins ist (V=1).

Es ergibt sich das vereinfachte Blockschaltbild in der folgenden Abbildung.

Rendered by QuickLaTeX.com

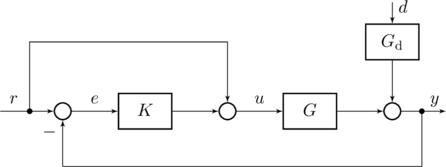
Abbildung 2: Standardregler mit Vorsteuerung und Störeingriff unter der (erlaubten) Annahme, dass die Strecke eine stationäre Verstärkung von eins hat.

Aus Abbildung 2 (als auch den Gleichungen (2)) wird deutlich, dass die stationäre Vorsteuerung den Sollwert unverändert auf den Streckeneingang gibt.

Es wird im Folgenden von dem Fall ausgegangen, dass die Strecke eine stationäre Einheitsverstärkung hat, also dass V=1 und Abbildung 2 gelten.

Grund 1: Sprungantworten werden überschwingen (und das ist doof)

So gut wie jeder Regler benötigt einen I-Anteil. Sagen wir: Jeder! Die Aufgabe des Integrators im Regler ist für stationäre Sollwertfolge zu sorgen, trotz (Eingangs-)störungen und Modellunsicherheiten. Anders gesagt: Der I-Anteil „lernt“ wieviel Stellgröße nötig ist, um die Regelstrecke stationär auf den Sollwert zu bringen.

Aber Moment! Genau das macht ja auch die Stationäre Vorsteuerung! (unter der Annahme, wir hätten keine Modellfehler oder Eingangsstörungen).

Es stellt sich die Frage, ob die beiden Teile Stationäre Vorsteuerung und I-Anteil (die dieselbe Aufgabe erfüllen), sich gegenseitig helfen, oder sich gegenseitig stören.

Die folgende Überlegung hilft uns, das herauszufinden.

Theorem (Satz): Wenn die Stationäre Vorsteuerung (mit einem Standardregler) verwendet wird und der Regler einen I-Anteil hat so schwingt die Sprungantwort über.

Beweis (umgangssprachlich formuliert, aber trotzdem gültig):

  1. Wir wissen, dass die Stationäre Vorsteuerung die Regelstrecke auf den Sollwert „hebt“. Anders gesagt: Im stationären Fall ist die Kombination von Vorsteuerung und Strecke gleich 1. Der Ausgang der Regelstrecke ist unabhängig vom Regler stationär gleich dem Sollwert (Regelfehler e = 0 für t \rightarrow \infty wenn r konstant ist).
  2. Das heißt, wir wissen, dass deshalb der I-Anteil irgendwann genau 0 ist — er hat ja nichts zu tun im stationären Fall. Also \lim_{t\rightarrow \infty} \int_0^t k\sr{I} e(\tau) d\tau = 0.
  3. Wir wissen auch, dass am Anfang der Sprungantwort, der Fehler e größer 0 ist. Zumindest kurzzeitig. Das heißt, dass der I-Anteil für eine gewisse Zeit größer null ist (er integriert den Regelfehler auf).
  4. Wenn der I-Anteil am Anfang der Sprungantwort positiv ist und am Ende der Sprungantwort (irgendwann) null ist, dann muss er zwischendrin negativ werden. Das geht aber nur, wenn der Regelfehler auch negativ wird.
  5. Fazit: Der Regelfehler wird negativ. Also muss der Ausgang y über dem Sollwert r liegen. Wir haben zwingend Überschwingen.

Wer nicht überzeugt ist und sich von Formeln mehr beeindrucken lässt, darf die Aussage und Argumentationskette natürlich gerne „mathematischer“ formulieren. Die Aussage bleibt dieselbe. Sie gilt jedoch nur solange, wie man nicht anfängt zu „schalten“ und z.B. den I-Anteil „resettiert“ (ein furchtbares Wort). Mehr zu den Verschlimmbesserungen später. Wir können aber hier schon sagen: Es wird nicht besser, nur schlimmer.

Ein Beispiel

Nehmen wir ein sehr einfaches „PT1“ System mit PI Standardregler.

(3)   \begin{align*} G(s) &= \frac{1}{s+1}\\ K(s) &= 1 + \frac1s. \end{align*}

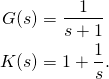
Die PI Verstärkungen sind also k\sr{P} = 1 und k\sr{I} = 1. Die Verstärkungen wurden so gewählt, dass die Zeitkonstante des geregelten Systems gleich der des ungeregelten Systems ist. Dieser Blog-Artikel hat nicht zum Ziel zu zeigen, wie gute Regler entworfen werden. Es ist bei einem PT1 ohne Randbedingungen wie Messrauschen, Störungen und Modellunsicherheiten nicht möglich einen realistischen Regler zu entwerfen. Hier könnte man, ohne realistische Randbedingungen, perfekte Regelung (also beliebig rasche Sollwertfolge) mit einem P-Regler erreichen. Nichtsdestotrotz ist es plausibel, dass man versucht ungefähr die Geschwindigkeit des ungeregelten Systems zu erreichen oder leicht zu übertreffen. Es soll gut genug sein, für unsere heutigen Überlegungen.

Dieses geschlossene System wurde mit Simulink nachgebildet. Einmal mit und einmal ohne Stationäre Vorsteuerung:

Simulation nur mit Standardregler
Simulation mit Stationärer Vorsteuerung

 

Schauen wir uns die Ergebnisse für einen Sollwertsprung bei t=1 sec an:

Simulation mit und ohne Stationäre Vorsteuerung

Die Ergebnisse bestätigen unsere Überlegungen von oben: Die Simulation mit Stationärer Vorsteuerung hat einen großen Überschwinger von 13,5%.

Jetzt könnte man behaupten: ,,Ja, aber die stationäre Vorsteuerung führt zu schnellerem Anstieg, also besserer Performance!“. Das ist Unsinn. Ja, die gelbe Linie steigt rascher an. Aber das könnte man genauso ohne die stationäre Vorsteuerung erreichen – nur mit dem PI, und zwar ohne Überschwingen! Das geht bei einem PT1 sehr einfach: Erhöhen wir die Reglerverstärkung von P und I-Anteil gleichmäßig. Es können beliebig rasche Sollwertfolgen erreicht werden, ohne Überschwingen. Ich zeige keinen weiteren Plot – es erscheint mir ein bisschen unsinnig beliebig rasche Sollwertfolgen zu simulieren.

Schauen wir uns nochmal die Simulationsergebnisse oben an: Bevor die gelbe Linie (Simulation mit Vorsteuerung) die blaue Linie (Sollwert) schneidet, wächst der I-Anteil des Reglers. Danach schwingt die gelbe Linie über und der I-Anteil baut sich wieder ab. Das ist die Visualisierung unseres Überschwingbeweises oben.

Ein Kommentar zur gängigen Praxis, den I-Anteil zu ,,resettieren“.

Die Stationäre Vorsteuerung wird, aus welchem schlechten Grund auch immer, tatsächlich oft verwendet. Was dann in der Praxis oft gemacht wird ist den I-Anteil beim Schneiden über dem Sollwert (Beginn des Überschwingens) auf null zu setzen. Das ist eine furchtbare Idee!

Wenn man den I-Anteil bei einem (fast) linearen System resettiert (noch immer ein furchtbares Wort), dann führt das zu einem schaltenden (hybriden, nichtlinearen) Regler. Einen nichtlinearen Regler für ein (fast) lineares System hinzubasteln ist, meiner Meinung nach, eine irrsinnig dumme Idee! Weil sie unnötig ist. So sieht man, dass eine schlechte Idee (Stationäre Vorsteuerung) viel schlimmere Korrekturmaßnahmen hervorbringen. Robustheitsbeweise? Vergessen Sie’s! Einfache Applikation? Vergessen Sie’s! Bei sicherheitskritischen Systemen? Wenn niemand verletzt wird, haben wir Glück. Bitte lassen Sie die Finger davon!

Fazit

Wir haben gezeigt, dass die Stationäre Vorsteuerung mit einem Standardregler immer zu Überschwingen der Sprungantwort führt. Ein Bild sagt mehr als tausend Worte und manche trauen der Simulation mehr als Formeln: Das Ergebnis einer Simulation – und zwar mit einem ,,PT1“ – also einer Regelstrecke, die ganz und gar nicht gerne schwingt, bestätigt unsere Warnung. Die Stationäre Vorsteuerung hat einen signifikanten und unnötigen Überschwinger produziert.

In den folgenden Blog-Artikeln schauen wir genauer hin:

  • Was bedeutet die Stationäre Vorsteuerung im allgemeinen Fall für die Performance der Sollwertfolge tatsächlich? Lohnt sie sich vielleicht doch?
  • Was bedeutet die Auslegung in der Praxis für die Störunterdrückung?
  • Wie geht man mit stationären Nichtlinearitäten (heben auf den Arbeitspunkt) korrekt um? Also ohne Stationäre Vorsteuerung, die alles schlimmer macht.

Gefällt Ihnen der Artikel? Schreiben Sie einen Kommentar. Gefällt er Ihnen nicht? Schreiben Sie einen Kommentar.

Literatur und Wissen

Empfehlenswerte Bücher sind zum Beispiel:

Alles zu modernem, praxisorientiertem Reglerentwurf finden Sie auch in unserem Seminar:

Moderner Reglerentwurf für die Praxis

 

Schlagwörter: , ,

Schreiben Sie einen Kommentar