In diesem Beitrag wollen wir ein Thema besprechen, welches eine zentrale Frage der experimentellen Modellbildung, der sog. Systemidentifikation, betrifft. Diese Frage ist die nach einem geeigneten Anregungssignal. In meiner industriellen Praxis bin ich im Kollegenkreis immer wieder auf eine einfache und auf den ersten Blick vielleicht sogar plausible Aussage gestoßen:
„Systemidentifikation machen wir mit Sprungantworten.“
Wir werden in diesem und den beiden folgenden Teilen gemeinsam erarbeiten, warum das im Allgemeinen eine schlechte Idee ist und kaum zu brauchbaren Modellen führen kann, sei es für einen Reglerentwurf, die Konzeption einer Fehlerdiagnose, oder sonst eine Anwendung eines dynamischen Systemmodells. Wer sich für den technischen Hintergrund nicht weiter interessiert, der darf gerne abkürzen und sich nur folgendes Einprägen:
Interessiert Sie die stationäre Verstärkung des Systems und sonst nichts? Dann können Sie Sprungantworten verwenden. Ansonsten sparen Sie sich die Zeit und die Kosten für die Messungen und deren Auswertung!
Um die Diskussion übersichtlich zu halten, beschränken wir uns auf Systeme mit einem Ein- und Ausgang, dem sog. SISO-Fall. Darüber hinaus betrachten wir lineare, zeitinvariante Systeme, bekannt unter der englischen Abkürzung LTI-Systeme, da diese zum einen theoretisch am einfachsten zugänglich sind und zum anderen für die industrielle Praxis bei weitem die größte Bedeutung haben. Die Erkenntnisse der folgenden Diskussion treffen aber auf nichtlineare Systeme ebenso zu, nur muss man sich hier noch mit zusätzlichen „Gemeinheiten“ der Theorie auseinandersetzen, ohne dass sich am Kern der Diskussion etwas ändern würde.
Streng genommen ist außerdem wohl kein System, mit dem sich ein Ingenieur oder Physiker in seiner Arbeit beschäftigt, ein wirkliches LTI-System, sondern es treten immer Eingangsbeschränkungen, Abhängigkeiten von Umgebungseinflüssen, oder Ähnliches auf. Die Erfolgsgeschichte der LTI-Systemtheorie seit den 1950er Jahren beruht darauf, dass sich die durch die Theorie beschriebene Klasse von Modellen auf reale, „schmutzige“ LTI-Systeme erfolgreich anwenden lässt – und dies sogar öfter, als man dies vielleicht zu hoffen gewagt hatte. Wir sprechen also von LTI-Modellen, mit welchen wir reale Systeme annähern.
Ein Motivationsbeispiel
Gehen wir davon aus, dass wir folgende Sprungantwort auf einen Eingangssprung der Höhe eins gemessen haben:
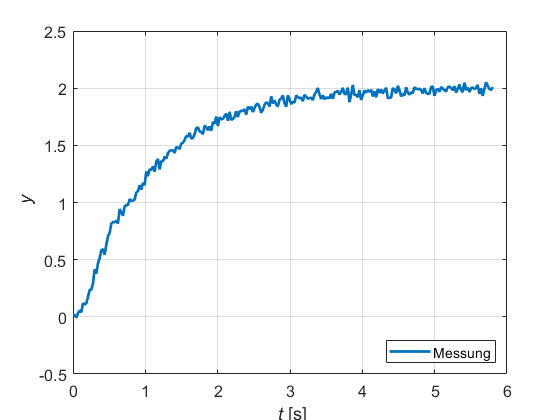
Wir nutzen nun ein beliebiges Optimierungsverfahren, um ein parametrisches Modell – in diesem Fall eine Übertragungsfunktion – zu finden, welches zu unserer Messung passt. Wir beginnen dabei vernünftigerweise mit einer möglichst einfachen Modellstruktur, dem sog. PT1-Glied. Wir sehen, dass wir dessen zwei Parameter Zeitkonstante und Verstärkungsfaktor so anpassen können, dass die Sprungantwort des Modells fast bis auf Strichstärke zu unserer Messung passt,
![]() .
.
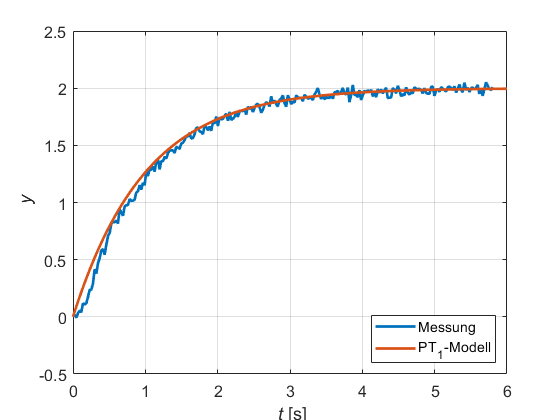
Violà, oder?
Nun ja, die stationäre Verstärkung unseres Systems von zwei spiegelt unser Modell auf jeden Fall wider. Aber in der Regel möchte man ja mehr, z.B. einen Reglerentwurf durchführen. Wir legen einen PI-Regler so aus, dass er die Zeitkonstante unseres Modells von 1s kompensiert und bei einem Führungsgrößensprung um eins eine Stellgrößenbeschränkung von drei eingehalten wird,
![]() .
.
In folgendem Bild sind die Sprungantworten der geschlossenen Regelkreise für unser PT1-Modell und das wahre System gegenübergestellt.
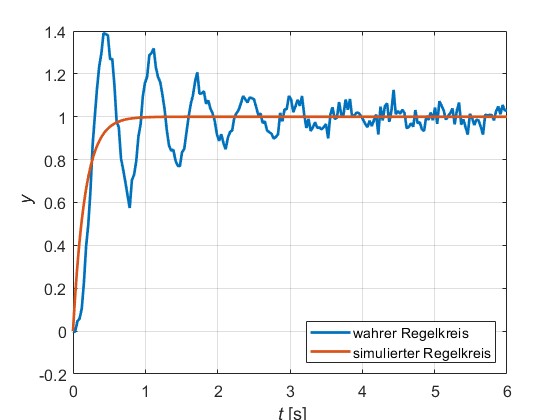
Im Gegensatz zur Simulation schwingt der wahre Regelkreis um 40% über und benötigt ca. fünfmal so lange, um in den Beharrungszustand zu kommen, wie vorausberechnet. Die Rauschunterdrückung ist schlecht. Hätte man die Reglerverstärkung beim Entwurf noch etwas größer gewählt, so wäre der Regelkreis am realen System sogar instabil gewesen!
Die Vorhersage mittels des Sprungantwort-Modells ist katastrophal.
Im wirklichen Arbeitsleben in der Industrie wird sich der zuständige Ingenieur von seinen Kollegen und Vorgesetzten nun die Frage gefallen lassen müssen, was denn solch ein modellbasierter Reglerentwurf taugt.
Wenn man kein Verständnis davon hat, was in obigem Beispiel schiefgelaufen ist, dann wird man – wie so oft im Alltagsgeschäft – eine systematische, sichere und daher absolut empfehlenswerte Vorgehensweise vorschnell über Bord werfen und Regler wieder von Hand einstellen. Das hat ja schon immer (mehr schlecht als recht) funktioniert.
Dabei lassen sich mit nur etwas mehr Wissen Fälle wie in obigem Beispiel sicher vermeiden und auch für komplexe Systeme systematisch leistungsfähige Regler entwerfen, wie es durch manuelles Einstellen niemals möglich wäre.
Wir werden in diesem und den weiteren beiden Teilen dieses Artikels ausleuchten, wo das Problem bei der obigen Vorgehensweise liegt und dass der Hauptgrund für das Scheitern die Verwendung von Sprungantworten bei der Systemidentifikation ist. Am Ende des zweiten Teils werden wir verstehen, was bei obigem Beispiel passiert ist.
Zur Erinnerung: Wie funktionieren LTI-Systeme?
Zu Beginn ist es hilfreich, sich noch einmal die wesentlichen Eigenschaften von LTI-Systemen ins Gedächtnis zu rufen. Das ist Kern jeder Grundlagenvorlesung Regelungstechnik und wer sich hier sattelfest fühlt, darf diesen Abschnitt natürlich gerne überspringen.
Auch hier machen wir wieder sinnvolle Einschränkungen: Wir betrachten nur vollständig steuer- und beobachtbare Systeme. Systemteile, welche nicht steuer- oder beobachtbar sind, sind anhand des Ein-Ausgangverhaltens des Systems nur schwer bzw. gar nicht identifizierbar. Zusätzlich fordern wir Stabilität, da ansonsten die Ausgangsgröße und zumindest ein Teil der internen Zustandsgrößen des Systems während der Systemidentifikation in konstruktionsbedingte/physikalische Begrenzungen laufen würden. Dies führt im besten Fall zur Verletzung der Annahme der Linearität und im schlechtesten Fall zu Sach- oder gar Personenschäden.
Unter den obigen Einschränkungen verhalten sich LTI-Systeme stets in folgender überschaubaren Weise: Wird, ausgehend von der Ruhelage bei null, der Systemeingang angeregt, so setzt sich der Systemausgang additiv aus zwei Anteilen zusammen:
- Dem Einschwingverhalten, dessen Amplitude asymptotisch gegen null geht und
- dem Stationärverhalten, welches sich wiederum additiv aus genau den Frequenzen des Eingangssignals zusammensetzt.
Besteht das Anregungssignal nur aus einer einzelnen Frequenz, also aus einer einzelnen Sinusschwingung, so antwortet das System stationär mit einer Sinusschwingung der gleichen Frequenz, aber mit im Allgemeinen anderer Amplitude und Phasenlage, als die Schwingung am Eingang.
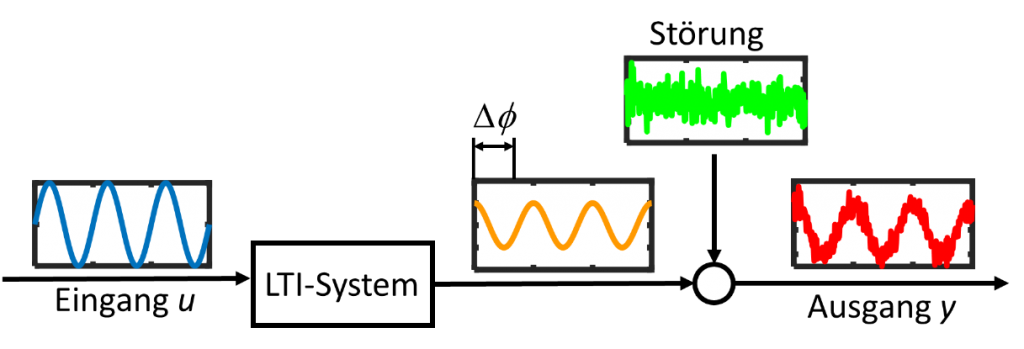
Kennt man die Werte der Amplituden- und Phasenänderung für alle Anregungsfrequenzen, so kennt man das gesamte Übertragungsverhalten des LTI-Systems.
Die geläufigste Darstellung dieses Ergebnisses ist das Bode-Diagramm. Der Charme der LTI-Theorie liegt nun darin, dass man nicht unendlich viele Messungen mit allen denkbaren Anregungsfrequenzen durchführen muss. Es genügt theoretisch, das System mit einem Anregungssignal zu beaufschlagen, welches alle relevanten Frequenzen enthält, da sich dem Systemausgang die Antworten auf alle Eingangsfrequenzen entnehmen lassen. Das Werkzeug, um die verschiedenen Frequenzanteile zu separieren, ist die Fourier- bzw. Spektralanalyse.
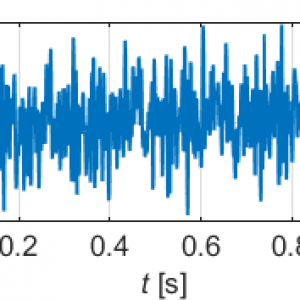
Die Grundlage der Spektralanalyse ist die Aussage, dass sich praktisch jedes Zeitsignal aus einer (in der Regel unendlich großen) Anzahl von harmonischen Komponenten, also Sinussignalen, additiv zusammensetzen lässt. Mit Hilfe der Spektralanalyse lassen sich die einzelnen Frequenzen und zugehörigen Amplituden der harmonischen Komponenten in einem Zeitsignal sichtbar machen, wie in folgendem Bild dargestellt:

Ohne jeweils eine Spektralanalyse für Ein- und Ausgangssignal durchführen zu müssen, wissen wir nun bereits aus der Theorie, dass im stationären Teil des Ausgangssignals (ohne Störung) keine Frequenzen enthalten sein können, welche nicht auch im Eingangssignal vorhanden waren!
Im nächsten Teil des Beitrags werden wir mit Hilfe der Spektralanalyse darlegen, warum die Sprungfunktion eine denkbar ungünstige Anregungsfunktion ist und warum die häufig genannten Gründe für die Verwendung von Sprungworten haltlos sind
Gefällt Ihnen der Artikel? Schreiben Sie einen Kommentar. Gefällt er Ihnen nicht? Schreiben Sie einen Kommentar.